Sphere Density Calculator

Sphere Density Calculator - Calculate radius and density of a sphere

Radius (m):

Density (kg/m³):

Density (g/cm³):

Density (oz/cu in):

Density (lb/cu in):

Density (lb/cu ft):

Density (lb/cu yd):

What is Sphere Density

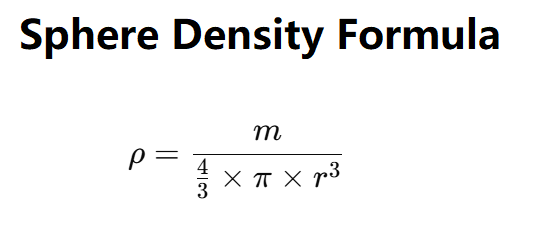
Sphere density is the mass per unit volume of a spherical object, typically measured in kg/m³. For a sphere, the density can be calculated from its mass and volume, where the volume is determined by the sphere’s radius using the formula \( V = \frac{4}{3} \pi r^3 \). The density is then \(\rho = \frac{m}{V}\). This calculator computes both the radius (if volume is provided) and the density based on the mass and volume of the sphere.

For example, a sphere with a mass of 25 kg and a volume of 5 m³ has a density of 5 kg/m³, and its radius can be derived from the volume.

How to Calculate Radius and Density of a Sphere

Density Calculation: The density is calculated using the formula:

\(\rho = \frac{m}{V}\)

Radius Calculation: The radius is calculated using the sphere volume formula:

\(V = \frac{4}{3} \pi r^3\)

Rearrange for radius: \(r = \left(\frac{3V}{4\pi}\right)^{1/3}\)

Where:

\(\rho\) = Density (kg/m³)
\(m\) = Mass (kg)
\(V\) = Volume (m³)
\(r\) = Radius (m)
\(\pi \approx 3.14159\)

Example Calculation: Let’s calculate based on the image example with a mass of 25 kg and a volume of 5 m³:

Density: \(\rho = \frac{25}{5} = 5 \, \text{kg/m³}\).
Radius: \( r = \left(\frac{3 \cdot 5}{4 \cdot \pi}\right)^{1/3} = \left(\frac{15}{12.56636}\right)^{1/3} \approx 1.0608 \, \text{m} \), which matches the image result.

Use the form above to input your mass and volume values with the desired units, and the calculator will compute the radius and density.

Density Units and Conversions

The SI unit for density is kilogram per cubic meter (kg/m³). Other convenient units include:

Gram per cubic centimeter (g/cm³): 1 g/cm³ = 0.001 kg/m³
Kilogram per liter (kg/L): 1 kg/L = 1000 kg/m³
Gram per milliliter (g/mL): 1 g/mL = 1000 kg/m³

Imperial units for density include:

Pound per cubic foot (lb/cu ft)
Pound per cubic yard (lb/cu yd): 1 lb/cu yd ≈ 0.037 lb/cu ft
Ounce per cubic inch (oz/cu in): 1 oz/cu in = 108 lb/cu ft
Pound per gallon (US) (lb/US gal): 1 lb/US gal ≈ 7.48 lb/cu ft

The calculator displays density in multiple units for convenience.

Standard Sphere Densities

Density varies depending on the material of the sphere. Some standard densities at room temperature (20 °C) include:

Water: \(\rho \approx 1000 \, \text{kg/m³}\)
Air: \(\rho \approx 1.225 \, \text{kg/m³}\)
Iron: \(\rho \approx 7870 \, \text{kg/m³}\)
Gold: \(\rho \approx 19300 \, \text{kg/m³}\)

Use this calculator to compare the density of your sphere against these standards.

What is the Radius of a Sphere?

The radius of a sphere is the distance from the center to any point on its surface. For a sphere, the volume is related to the radius by \( V = \frac{4}{3} \pi r^3 \), allowing the radius to be calculated if the volume is known.

FAQs

How do you calculate the radius of a sphere from volume?

To calculate the radius:

Measure the volume \( V \) in cubic meters (m³).
Use the formula: \( r = \left(\frac{3V}{4\pi}\right)^{1/3} \).

What is the density of a sphere with mass 25 kg and volume 5 m³?

The density is \(\rho = \frac{25}{5} = 5 \, \text{kg/m³}\), and the radius is approximately 1.0608 m, as shown in the image.